 |
The basic idea is quite simple and explained in a few words:
Everything, even numbers and strings, is stored as nodes of a Directed Acyclic Graph (DAG).
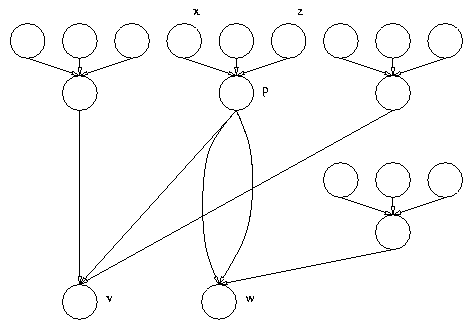
The following excerpt from an input file creates the graph shown in figure 3.1 (you can alse use the Graph-Editor (2.5) for exploring the created graph):
Example 2: (taken from: data/examples/syntax_ok.dat (7.42))
x = 1; z = 4; p = (x,1,z); v = ( (1,1,1), p, (2,31,0) ); w = ( p, p, (1,17,4) );
This example also shows the use of variables. Variables are just substitutes for nodes of the DAG, and can be used at any place where a graph node is expected.
They also increment the reference counters of the nodes to which they point, and thus prevent the deletion of otherwise unreferenced nodes. For example the following statement is quite useless
1;
since it would temporarily create a number node with value 1, but delete it immediately afterwards, since it is referenced by no other node.