5.4 Trimmed Nurbs Surfaces

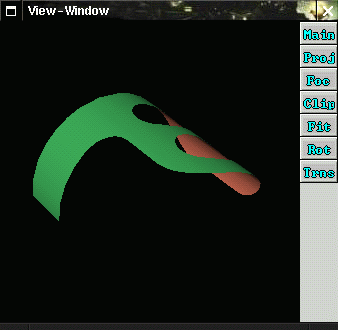
In Example 11 the same surface as in Example 8 is created, but this time with three trim regions formed out of 8 2D polylines and nurbs curves. The result is shown in figure 5.8.

Example 11: (taken from: data/examples/nurbsurf3.dat (7.28))

/* 
 *  nurbs surface 
 */
surf1 = NURBSURF( 
  (0., 0., 1., 1.),
  (0., 0., 0., 0.5, 0.5, 1., 1., 1.),
  (
    ((5., 0.,  0., 0.5), (5., 5.,  0., 0.5)),
    ((5., 0., 2.5, 0.5), (5., 5., 2.5, 0.5)),
    ((5., 0.,  5., 1.),  (5., 10., 5., 1.)),
    ((0., 0., 2.5, 0.5), (0., 5., 2.5, 0.5)),
    ((0., 0.,  0., 0.5), (0., 5.,  0., 0.5))   
  )
);

/* 
 *  first region 
 */
con1 = POLYLINE2(
  ((0.,0.7), (0.,0.), (0.3,0.0), (0.3,0.25))
);
con2 = NURBCURV2(
  (0., 0., 0., 1., 1., 1.),
  (
    (0.15,0.125,0.5),  /* (0.3,0.25) */
    (0.15,0.2,0.5),    /* (0.3,0.4)  */
    (0.45,0.4,1.0)
  )
);
con3 = POLYLINE2(
  ((0.45,0.4), (0.7,0.4))
);
con4 = NURBCURV2(
  (0., 0., 0., 0.5, 0.5, 1., 1., 1.),
  (
    (0.35,0.2,0.5),  /* (0.7,0.4) */
    (0.5,0.2,0.5),   /* (1.0,0.4) */
    (1.0,0.7,1.0),
    (0.5,0.5,0.5),   /* (1.0,1.0) */
    (0.35,0.5,0.5)   /* (0.7,1.0) */
  )
);
con5 = POLYLINE2(
  ((0.7,1.0), (0.3,1.0))
);
con6 = NURBCURV2(
  (0., 0., 0., 1., 1., 1.),
  (
    (0.15,0.5,0.5),  /* (0.3,1.0) */
    (0.0,0.5,0.5),   /* (0.0,1.0) */
    (0.0,0.7,1.0)
  )
);
reg1 = REGION( (con1,con2,con3,con4,con5,con6) );

/* 
 *  second region
 */
con7 = NURBCURV2( 
  (0., 0., 0., 0.25, 0.25, 0.5, 0.5, 0.75, 0.75, 1., 1., 1.),
  (
    (0.3,0.55,1.0),
    (0.075,0.275,0.5),  /* (0.15,0.55) */
    (0.075,0.35,0.5),    /* (0.15,0.7)  */
    (0.075,0.425,0.5),   /* (0.15,0.85) */
    (0.3,0.85,1.0),
    (0.225,0.425,0.5),  /* (0.45,0.85) */
    (0.225,0.35,0.5),   /* (0.45,0.7)  */
    (0.225,0.275,0.5),  /* (0.45,0.55) */
    (0.3,0.55,1.0)
  )
);
reg2 = REGION( (con7) );

/*
 *  third region
 */
con8 = NURBCURV2( 
  (0., 0., 0., 0.25, 0.25, 0.5, 0.5, 0.75, 0.75, 1., 1., 1.),
  (
    (0.7,0.55,1.0),
    (0.275,0.275,0.5),  /* (0.55,0.55) */
    (0.275,0.35,0.5),   /* (0.55,0.7)  */
    (0.275,0.425,0.5),  /* (0.55,0.85) */
    (0.7,0.85,1.0),
    (0.425,0.425,0.5),  /* (0.85,0.85) */
    (0.425,0.35,0.5),   /* (0.85,0.7)  */
    (0.425,0.275,0.5),  /* (0.85,0.55) */
    (0.7,0.55,1.0)
  )
);
reg3 = REGION( (con8) );

/* 
 *  trimmed nurbs surface 
 */
part1 = PARTITION( (reg1,reg2,reg3) );
trimsurf1 = TNURBSURF( part1, surf1 );

Figure 5.8: Cylinder Half with 3 trim contours

When forming regions out of multiple trim elements, the end point of one element must be equal to the start point of the next element. So it often is neccessary to invert the orientation of a polyline or nurbs curve, so that the elements fit together.

This can be done via the keywords NURBSUBC and POLYLINESUB. These constructs are for extracting subranges of nurbs curves and polylines, but they also invert the orientation of curves and polylines, when the ``lower'' bound of the subrange is bigger then the ``upper'' bound (for polylines the bounds are vertex numbers, and for nurbs surface locations in the parametric domain).

This is illustrated in Example 12.

Example 12: (taken from: data/examples/nurbsurf4.dat (7.29))

/* 
 *  first region 
 */
con1 = POLYLINE2(
  ((0.,0.7), (0.,0.), (0.3,0.0), (0.3,0.25))
);
wrong_con2 = NURBCURV2(
  (0., 0., 0., 1., 1., 1.),
  (
    (0.45,0.4,1.0),
    (0.15,0.2,0.5),    /* (0.3,0.4)  */
    (0.15,0.125,0.5)   /* (0.3,0.25) */
  )
);
con2 = NURBSUBC2(
  (1,0),
  wrong_con2
);
con3 = POLYLINE2(
  ((0.45,0.4), (0.7,0.4))
);
con4 = NURBCURV2(
  (0., 0., 0., 0.5, 0.5, 1., 1., 1.),
  (
    (0.35,0.2,0.5),  /* (0.7,0.4) */
    (0.5,0.2,0.5),   /* (1.0,0.4) */
    (1.0,0.7,1.0),
    (0.5,0.5,0.5),   /* (1.0,1.0) */
    (0.35,0.5,0.5)   /* (0.7,1.0) */
  )
);
wrong_con5 = POLYLINE2(
  ((0.3,1.0), (0.7,1.0))
);
con5 = POLYLINESUB2(
  (1,0),
  wrong_con5
);
con6 = NURBCURV2(
  (0., 0., 0., 1., 1., 1.),
  (
    (0.15,0.5,0.5),  /* (0.3,1.0) */
    (0.0,0.5,0.5),   /* (0.0,1.0) */
    (0.0,0.7,1.0)
  )
);
reg1 = REGION( (con1,con2,con3,con4,con5,con6) );