 |
In this section two examples of global and local surface interpolation, one example of global surface approximation, and two examples of multi level bspline approximation are given. The first three algorithms are the equivalents for surfaces to the algorithms from the previous two sections for curves, the last one will be described in more detail in the next section.
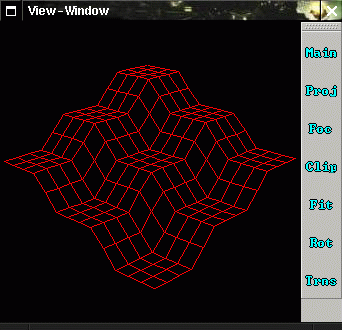
In all examples the same data point set is used. It is shown in Figure 5.19 (the code with which Figure 5.19 was created can be found in Example 20).
Example 20: (taken from: data/examples/surf_testcase.dat (7.41))
points1 = POINTMATRIX(
/* matrix of data points: */
(
((0,0,0),(1,0,0),(2,0,0),(3,0,0), (4,0,1),
(5,0,2),(6,0,2),(7,0,2),(8,0,2), (9,0,3),
(10,0,4),(11,0,4),(12,0,4),(13,0,4)),
((0,1,0),(1,1,0),(2,1,0),(3,1,0), (4,1,1),
(5,1,2),(6,1,2),(7,1,2),(8,1,2), (9,1,3),
(10,1,4),(11,1,4),(12,1,4),(13,1,4)),
((0,2,0),(1,2,0),(2,2,0),(3,2,0), (4,2,1),
(5,2,2),(6,2,2),(7,2,2),(8,2,2), (9,2,3),
(10,2,4),(11,2,4),(12,2,4),(13,2,4)),
((0,3,0),(1,3,0),(2,3,0),(3,3,0), (4,3,1),
(5,3,2),(6,3,2),(7,3,2),(8,3,2), (9,3,3),
(10,3,4),(11,3,4),(12,3,4),(13,3,4)),
((0,4,1),(1,4,1),(2,4,1),(3,4,1), (4,4,2),
(5,4,3),(6,4,3),(7,4,3),(8,4,3), (9,4,4),
(10,4,5),(11,4,5),(12,4,5),(13,4,5)),
((0,5,2),(1,5,2),(2,5,2),(3,5,2), (4,5,3),
(5,5,4),(6,5,4),(7,5,4),(8,5,4), (9,5,5),
(10,5,6),(11,5,6),(12,5,6),(13,5,6)),
((0,6,2),(1,6,2),(2,6,2),(3,6,2), (4,6,3),
(5,6,4),(6,6,4),(7,6,4),(8,6,4), (9,6,5),
(10,6,6),(11,6,6),(12,6,6),(13,6,6)),
((0,7,2),(1,7,2),(2,7,2),(3,7,2), (4,7,3),
(5,7,4),(6,7,4),(7,7,4),(8,7,4), (9,7,5),
(10,7,6),(11,7,6),(12,7,6),(13,7,6)),
((0,8,2),(1,8,2),(2,8,2),(3,8,2), (4,8,3),
(5,8,4),(6,8,4),(7,8,4),(8,8,4), (9,8,5),
(10,8,6),(11,8,6),(12,8,6),(13,8,6)),
((0,9,3),(1,9,3),(2,9,3),(3,9,3), (4,9,4),
(5,9,5),(6,9,5),(7,9,5),(8,9,5), (9,9,6),
(10,9,7),(11,9,7),(12,9,7),(13,9,7)),
((0,10,4),(1,10,4),(2,10,4),(3,10,4), (4,10,5),
(5,10,6),(6,10,6),(7,10,6),(8,10,6), (9,10,7),
(10,10,8),(11,10,8),(12,10,8),(13,10,8)),
((0,11,4),(1,11,4),(2,11,4),(3,11,4), (4,11,5),
(5,11,6),(6,11,6),(7,11,6),(8,11,6), (9,11,7),
(10,11,8),(11,11,8),(12,11,8),(13,11,8)),
((0,12,4),(1,12,4),(2,12,4),(3,12,4), (4,12,5),
(5,12,6),(6,12,6),(7,12,6),(8,12,6), (9,12,7),
(10,12,8),(11,12,8),(12,12,8),(13,12,8)),
((0,13,4),(1,13,4),(2,13,4),(3,13,4), (4,13,5),
(5,13,6),(6,13,6),(7,13,6),(8,13,6), (9,13,7),
(10,13,8),(11,13,8),(12,13,8),(13,13,8))
)
);
SCENEROOT = SCENENODE (
(),
(),
(points1)
);
In Example 21 the point set is interpolated by a surface of degree 3*3 by using Global Interpolation. The result is shown in Figure 5.20.
Example 21: (taken from: data/examples/nubgis1.dat (7.16))
surf1 = NUBGIS( 3, /* degree U */ 3, /* degree V */ points1 /* matrix of data points */ );
In Example 22 the point set is interpolated by a bicubic surface using Local Bicubic Interpolation. The result is shown in Figure 5.21.
Example 22: (taken from: data/examples/nublbis1.dat (7.18))
surf1 = NUBLBIS( 0, /* preserve corner flag */ points1 /* matrix of data points */ );
In Example 23 the point set is approximated by a surface of degree 3*3 with 10*10 control points by using Global Approximation. The result is shown in Figure 5.22.
Example 23: (taken from: data/examples/nubgas1.dat (7.14))
surf1 = NUBGAS( 3, /* degree U */ 10, /* number of control points for U */ 3, /* degree V */ 10, /* number of control points for V */ points1 /* matrix of data points */ );
In Example 24 and 25 the point set is approximated by surfaces of degree 3*3 via Multi Level B-Spline Approximation. The number of iterations is 4 in Example 24 and 5 in Example 25. The results are shown in Figure 5.23 and 5.24.
Example 24: (taken from: data/examples/nubmbas1.dat (7.19))
surf1 = NUBMBAS(
4, /* number of iterations */
0, /* minimize area of base rectangle in XY-plane */
3, /* degree in U-direction the surface shall have */
3, /* degree in V-direction the surface shall have */
/* list of data points: */
plist1 = (
(0,0,0),(1,0,0),(2,0,0),(3,0,0), (4,0,1),
(5,0,2),(6,0,2),(7,0,2),(8,0,2), (9,0,3),
(10,0,4),(11,0,4),(12,0,4),(13,0,4),
(0,1,0),(1,1,0),(2,1,0),(3,1,0), (4,1,1),
(5,1,2),(6,1,2),(7,1,2),(8,1,2), (9,1,3),
(10,1,4),(11,1,4),(12,1,4),(13,1,4),
(0,2,0),(1,2,0),(2,2,0),(3,2,0), (4,2,1),
(5,2,2),(6,2,2),(7,2,2),(8,2,2), (9,2,3),
(10,2,4),(11,2,4),(12,2,4),(13,2,4),
(0,3,0),(1,3,0),(2,3,0),(3,3,0), (4,3,1),
(5,3,2),(6,3,2),(7,3,2),(8,3,2), (9,3,3),
(10,3,4),(11,3,4),(12,3,4),(13,3,4),
(0,4,1),(1,4,1),(2,4,1),(3,4,1), (4,4,2),
(5,4,3),(6,4,3),(7,4,3),(8,4,3), (9,4,4),
(10,4,5),(11,4,5),(12,4,5),(13,4,5),
(0,5,2),(1,5,2),(2,5,2),(3,5,2), (4,5,3),
(5,5,4),(6,5,4),(7,5,4),(8,5,4), (9,5,5),
(10,5,6),(11,5,6),(12,5,6),(13,5,6),
(0,6,2),(1,6,2),(2,6,2),(3,6,2), (4,6,3),
(5,6,4),(6,6,4),(7,6,4),(8,6,4), (9,6,5),
(10,6,6),(11,6,6),(12,6,6),(13,6,6),
(0,7,2),(1,7,2),(2,7,2),(3,7,2), (4,7,3),
(5,7,4),(6,7,4),(7,7,4),(8,7,4), (9,7,5),
(10,7,6),(11,7,6),(12,7,6),(13,7,6),
(0,8,2),(1,8,2),(2,8,2),(3,8,2), (4,8,3),
(5,8,4),(6,8,4),(7,8,4),(8,8,4), (9,8,5),
(10,8,6),(11,8,6),(12,8,6),(13,8,6),
(0,9,3),(1,9,3),(2,9,3),(3,9,3), (4,9,4),
(5,9,5),(6,9,5),(7,9,5),(8,9,5), (9,9,6),
(10,9,7),(11,9,7),(12,9,7),(13,9,7),
(0,10,4),(1,10,4),(2,10,4),(3,10,4), (4,10,5),
(5,10,6),(6,10,6),(7,10,6),(8,10,6), (9,10,7),
(10,10,8),(11,10,8),(12,10,8),(13,10,8),
(0,11,4),(1,11,4),(2,11,4),(3,11,4), (4,11,5),
(5,11,6),(6,11,6),(7,11,6),(8,11,6), (9,11,7),
(10,11,8),(11,11,8),(12,11,8),(13,11,8),
(0,12,4),(1,12,4),(2,12,4),(3,12,4), (4,12,5),
(5,12,6),(6,12,6),(7,12,6),(8,12,6), (9,12,7),
(10,12,8),(11,12,8),(12,12,8),(13,12,8),
(0,13,4),(1,13,4),(2,13,4),(3,13,4), (4,13,5),
(5,13,6),(6,13,6),(7,13,6),(8,13,6), (9,13,7),
(10,13,8),(11,13,8),(12,13,8),(13,13,8)
)
);
Example 25: (taken from: data/examples/nubmbas2.dat (7.20))
surf1 = NUBMBAS( 5, /* number of iterations */ 0, /* minimize area of base rectangle in XY-plane */ 3, /* degree in U-direction the surface shall have */ 3, /* degree in V-direction the surface shall have */ plist1 /* list of data points */ );